
나이브베이즈(Naive Bayes)
사건 B가 주어졌을 때 사건 A가 일어날 확률인 P(A|B), 조건부 확률과 베이즈 정리를 이용한 알고리즘
나이브(Naive)는 예측에 사용되는 특성치(X)가 상호 독립적이라는 가정하에 확률 계산을 단순화하기 위해 나이브(단순/순진한 가정)이라고 이름이 붙은 것이다. (모든 특성치들이 동등한 역할)
베이즈(Bayes)는 특성치(X)가 클래스 전체의 확률 분포에 대비하여 특정 클래스에 속할 확률을 베이즈 정리를 기반으로 계산한 것이다.
설명이 어려워서 그냥 그러려니 하고 넘어감
scikit-learn
분류문제에 사용되는 나이브베이즈는 사이킷런의 naive_bayes에 있다.
그 중 분류 문제에서는 가우시안 나이브베이즈(GaussianNB) 알고리즘을 주로 사용한다.
GaussianNB의 주요 하이퍼파라미터는 var_smoothing이다.
회귀문제는 linear_model의 Baysian regressors을 활용하는 것이 좋다.
그 중 BayesianRidge 모델이 가장 적합하다.
BayesianRidge 모델의 하이퍼파라미터는 alpha_1과 lambda_1이다.
이것도 내용이 어려워서 그냥 그러려니 하고 넘어감
Part1. 분류(Classification)
1) 데이터셋 나누기, 정규화
import warnings
warnings.filterwarnings("ignore")
import pandas as pd
data=pd.read_csv('breast-cancer-wisconsin.csv', encoding='utf-8')
X=data[data.columns[1:10]]
y=data[["Class"]]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
#min-max 정규화
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(X_train)
X_scaled_train = scaler.transform(X_train)
X_scaled_test = scaler.transform(X_test)breast-cancer-wisconsin.csv파일로 나이브 베이즈 분류 실습 시작!
이제 데이터셋 불러오고, train_test_split해주고, 정규화하는 과정은 교재에서 그냥 건너뛴다.
앞에서 했던 코드 재탕이라 복붙으로 긁어왔다.
2) 기본 모델 적용
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X_scaled_train, y_train)
pred_train = model.predict(X_scaled_train)
model.score(X_scaled_train, y_train)sklearn.naive_bayes로부터 GaussianNB 라이브러리를 가져왔다.
model 변수를 GaussianNB()로 설정해주어, 모델 정확도까지 체크하는 코드이다.
3) 혼동행렬, 분류예측 레포트
#혼동행렬
from sklearn.metrics import confusion_matrix
confusion_train = confusion_matrix(y_train, pred_train)
#정상을 예측하는 정확도가 다른 알고리즘에 비해 떨어진다.
print("훈련데이터 오차행렬:\n", confusion_train)
정상을 예측하는 정확도가 다른 알고리즘에 비해 떨어지는 것을 확인할 수 있다.
#분류예측 레포트
from sklearn.metrics import classification_report
cfreport_train = classification_report(y_train, pred_train)
print("분류예측 레포트:\n", cfreport_train)분류예측 레포트까지 확인했다.
test 데이터도 똑같이 혼동행렬, 분류예측 레포트를 확인해준다.
4) Grid Search
#Grid Search
param_grid = {'var_smoothing' : [0,1,2,3,4,5,6,7,8,9,10]}
from sklearn.model_selection import GridSearchCV
grid_search = GridSearchCV(GaussianNB(), param_grid, cv=5)
grid_search.fit(X_scaled_train, y_train)
print("Best Parameter: {}".format(grid_search.best_params_))
print("Best Scroe: {:.4f}".format(grid_search.best_score_))
print("TestSet Score: {:.4f}".format(grid_search.score(X_scaled_test, y_test)))
하이퍼파라미터 var_smoothing을 0부터 10까지 총 11개로 설정하여 그리드탐색을 진행했다.
탐색 결과, 최적의 하이퍼파라미터는 var_smoothing = 0일 때로 나타났다.
5) Random Search
#Random Search
from scipy.stats import randint
param_distribs = {'var_smoothing': randint(low=0, high=20)}
from sklearn.model_selection import RandomizedSearchCV
random_search = RandomizedSearchCV(GaussianNB(), param_distributions=param_distribs, n_iter=100, cv=5)
random_search.fit(X_scaled_train, y_train)
print("Best Parameter: {}".format(random_search.best_params_))
print("Best Score: {:.4f}".format(random_search.best_score_))
print("TestSet Score: {:.4f}".format(random_search.score(X_scaled_test, y_test)))
랜덤서치로 하이퍼파라미터의 var_smoothing을 0부터 20까지 중에서 랜덤으로, 100번 수행하게 했다.
역시 var_smoothing = 0일때 가장 좋은 결과를 나타냈다.
Part2. 회귀(Regression)
Part2. 회귀는 갑자기 알 수 없는 에러로 인해 실습하다 중단해버렸다.
분명 이전에선 멀쩡히 잘 작동하던 코드인데 말이다.
1)데이터셋 나누기, 정규화
import pandas as pd
data2 = pd.read_csv('house_price.csv', encoding='utf=8')
X=data2[data2.columns[1:5]]
y=data2[["house_value"]]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 42)
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(X_train)
X_scaled_train = scaler.transform(X_train)
X_scaled_test = scaler.transform(X_test)Regression 회귀 분석은 이전에 주택가격(house_price.csv) 파일로 실습!
2) 기본 모델 적용
#Part2. 회귀(Regression)
from sklearn.linear_model import BayesianRidge
model=BayesianRidge()
model.fit(X_scaled_train, y_train)
pred_train = model.predict(X_scaled_train)
model.score(X_scaled_train, y_train)
pred_test = model.predict(X_scaled_test, y_test)
model.score(X_scaled_test, y_test)sklearn.linear_model의 BayesianRidge 라이브러리를 사용하여 모델 정확도를 계산해보았다.
3) 오차 RMSE 계산
import numpy as np
from sklearn.metrics import mean_squared_error
MSE_train = mean_squared_error(y_train, pred_train)
MSE_test = mean_squared_error(y_test, pred_test)
print("훈련데이터 RMSE:", np.sqrt(MSE_train))
print("테스트데이터 RMSE:", np.sqrt(MSE_test))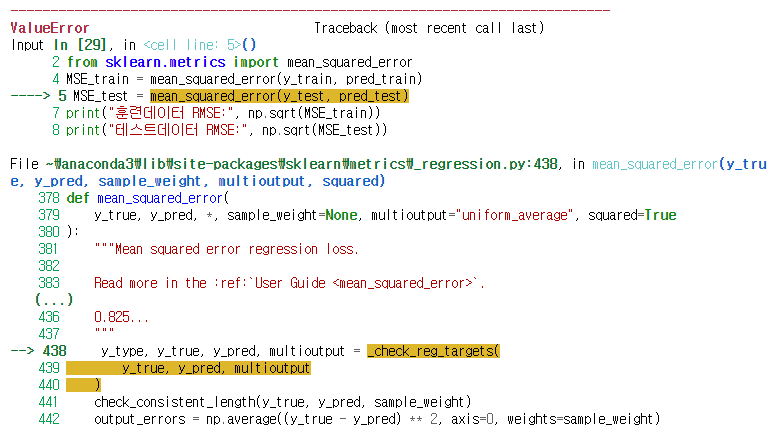
sklearn.metrics의 mean_squared_error 라이브러리를 불러와 RMSE를 계산하다 에러가 났다.
MSE_train은 멀쩡히 작동하는데, MSE_test 코드에서 말썽이다.
Grid Search, Random Search에서 하이퍼파라미터 alpha_1, lambda_1 설정하는것도 해봐야하는데 여기서 중단,
나중에 시간되면 다시 천천히 살펴보아야겠다.
'자기계발 > Python' 카테고리의 다른 글
| [빅데이터분석기사] 17 서포트 벡터머신 (0) | 2022.06.22 |
|---|---|
| [빅데이터분석기사] 16 인공신경망 (0) | 2022.06.21 |
| [빅데이터분석기사] 14 K-최근접이웃법(KNN) (0) | 2022.06.21 |
| [빅데이터분석기사] 13 로지스틱 회귀모델 (0) | 2022.06.20 |
| [빅데이터분석기사] 12 다중분류 (0) | 2022.06.20 |