
혼공단 9기 4주차 학습 내용 정리
이번 챕터는 통계, 그래프에 대한 기본적인 내용을 다뤄서 저번주에 비해 내용이 정말 쉬웠다!
데이터 관련 자격증 공부를 하면서 한번 씩 배웠던 내용이라 금방 공부할 수 있었다.
주말에는 약속이 있으니까 얼렁 포스팅하고 숙제 제출해야지~!
보내주신 메가커피 크로플 맛있게 먹겠습니다. 감사합니당😊
Chapter 04 데이터 요약하기

4-1 통계로 요약하기
기술통계 구하기 : describe() 메서드
ns_book6.describe()
ns_book7 = ns_book6[ns_book6['도서권수']>0]
ns_book7.describe(percentiles=[0.3, 0.6, 0.9])
ns_book7.describe(include='object')describe() 메서드를 호출하면 기본적인 몇 가지 기술통계(count, mean, std, min, 25%, 50%, 75%, max)를 보여준다.
여기서 count 값은 누락된 값을 제외한 데이터 개수를 나타낸다.
기본적으로는 25%, 75%에 해당하는 값(사분위수)를 보여주지만, percentiles 매개변수를 사용하면 원하는 위치의 값을 보는 것이 가능하다.
include 매개변수는 수치가 아닌 다른 데이터 타입의 열을 보고 싶을 때 사용한다.
다양한 기술통계값
ns_book7['대출건수'].mean() #평균 구하기
ns_book7['대출건수'].median() #중앙값 구하기
ns_book7['대출건수'].drop_duplicates().median() #중복값 제거 후 중앙값 구하기
ns_book7['대출건수'].min() #최솟값 구하기
ns_book7['대출건수'].max() #최댓값 구하기
ns_book7['대출건수'].quantile(0.25) #분위수 값 구하기
ns_book7['대출건수'].quantile([0.25, 0.5, 0.75]) #분위수 값 여러 개 구하기
pd.Series([1,2,3,4,5]).quantile(0.9) #특수 상황의 분위수
ns_book7['대출건수'].var() #분산 구하기
ns_book7['대출건수'].std() #표준편차 구하기
ns_book7['도서명'].mode() #최빈값 구하기분위수를 구하는 quantile() 메서드
quantile() 메서드에서 interpolation 매개변수는 중간 값을 계산하는 방법을 결정한다.
interpolation의 디폴트 값은 양쪽 분위수에 비례하여 결정되는 'linear' 이며 'midpoint'로 설정시 분위수에 상관없이 무조건 두 수 사이의 중앙값을 반환한다. 'nearest' 옵션은 두 수 중 가까운 값을 선택한다.
데이터프레임에서 기술통계 구하기
ns_book7.mean(numeric_only=True)
ns_book7.loc[:,'도서명':].mode()수치형 열만 연산할 수 있게 numeric_only 매개변수를 True로 지정해주어야 한다.
지정하지 않을 시 모든 데이터 타입의 열에 대해 연산을 수행하기 때문에 시간도 오래걸리고 에러가 발생한다.
넘파이 기술통계 함수
1) 평균구하기 - mean(), average() 차이
import numpy as np
np.mean(ns_book7['대출건수'])
np.average(ns_book7['대출건수'], weights=1/ns_book7['도서권수'])average() 함수는 mean()과 동일하게 평균을 구하는 기능을 하는데, weights 매개변수를 사용하면 가중치가 포함된 평균을 구할 수 있다. 이 것을 가중 평균이라고 한다.
2) 중앙값(median), 최솟값(min), 최댓값(max), 분위수(quantile), 표준편차(std) 함수로 각각 동일
3) 분산구하기 - var()
np.var(ns_book7['대출건수']) #결과 371.6946438971496
ns_book7['대출건수'].var() #결과 371.69563042906674
ns_book7['대출건수'].var(ddof=0) #판다스 ddof 디폴트값 1
np.var(ns_book7['대출건수'], ddof=1) #넘파이 ddof 디폴트값 0넘파이와 판다스로 var() 메서드로 분산을 구할 때 각각 값이 다르게 나오는 이유는 자유도 때문이다.
판다스는 분산을 구할 때 n-1로 나눠주고, 넘파이는 n으로 나눠준다.
* n이 아닌 n-1로 나누는 이유 : 표본집단은 평균과 n-1개의 샘플 데이터를 아고 있다면 마지막 한 개의 샘플 값을 자동으로 알 수 있기 때문이다. 표본집단으로 모집단의 특징을 추정하려는 것이 아니라면 n으로 나눠주면 된다.
판다스와 넘파이 모두 ddof 매개변수로 자유도 차감값을 지정하는 것이 가능하다.
4) 최빈값 구하기
#넘파이 최빈값 구하기
values, counts = np.unique(ns_book7['도서명'], return_counts=True)
max_idx = np.argmax(counts)
values[max_idx]넘파이에선 최빈값을 계산하는 함수를 제공해주지 않기 때문에 배열에서 고유한 값을 찾아주는 unique() 함수로 찾아준다. return_counts 매개변수(기본값 False)를 True로 지정해주면 고유한 값의 등장 횟수를 반환한다.
argmax() 함수를 사용하여반환된 값들 중 가장 큰 값의 인덱스를 받아오면 최빈값을 구할 수 있다.
4-2 분포 요약하기
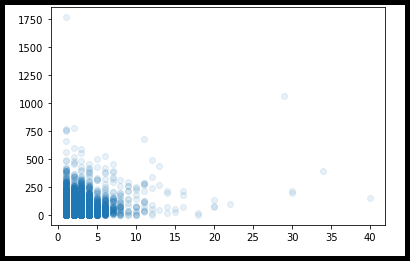
1. 산점도 그리기 - scatter() 함수
산점도 : 두 변수 혹은 두 가지 특성 값을 직교 좌표계에 점으로 나타낸 그래프
import matplotlib.pyplot as plt
#plt.scatter(ns_book7['번호'], ns_book7['대출건수'])
plt.scatter(ns_book7['도서권수'], ns_book7['대출건수'], alpha=0.1)
plt.show()scatter() 함수를 사용하여 산점도를 그릴 수 있다.
alpha 매개변수는 좌표계에 찍히는 점의 투명도를 조절하는 역할을 한다. (0에 가까울 수록 투명하고, 1에 가까울수록 불투명해진다.)
2. 히스토그램 그리기 - hist() 함수
히스토그램 : 수치형 특성의 값을 일정한 구간으로 나누어 구간 안에 포함된 데이터 개수를 막대 그래프로 그린 것
#히스토그램 구간 개수 지정 - bins 매개변수
#plt.hist([0,3,5,6,7,7,9,13], bins=5)
#plt.show()
#히스토그램 구간 확인 - histogram_bin_edges() 함수
import numpy as np
np.histogram_bin_edges([0,3,5,6,7,7,9,13], bins=5)
#난수 생성
np.random.seed(42)
random_samples = np.random.randn(1000)
#plt.hist(random_samples)
#구간 조정 - yscale() 함수
#plt.hist(ns_book7['대출건수'])
#plt.yscale('log')
#plt.show()
#도서명 길이로 그린 히스토그램
title_len = ns_book7['도서명'].apply(len)
plt.hist(title_len, bins=100)
plt.show()◾ bins 매개변수 : 히스토그램 구간은 기본적으로 10개이지만, bins 매개변수로 구간 개수를 지정할 수 있다.
◾ histogram_bin_edges() 함수 : 히스토그램 구간의 경계값을 출력할 수 있다.
◾ randn() 함수 : 표준정규분포를 따르는 랜덤한 실수를 생성한다. seed() 함수를 사용하면 고정된 유사난수를 생성한다.
◾ yscale() 함수 : 특정 구간의 도수가 너무 커서 다른 구간은 표시되지 않는다면 로그 함수를 적용하여 해결이 가능하다. 함수 안에 'log'를 지정하면 로그 스케일로 바꿀 수 있고, x축도 동일하게 xscale() 함수를 사용할 수 있다.
( hist()함수는 log 매개변수를 제공하기 때문에 yscale() 굳이 사용 안해도 되긴 함 )
마지막 코드는 apply() 메서드로 파이썬의 len() 함수를 적용하여 도서명 길이를 추출한 코드이다.

3. 상자 수염 그림 그리기 - boxplot() 함수
상자 수염 그림 : 최솟값, 세 개의 사분위수, 최댓값까지 다섯 개의 숫자를 사용해 데이터를 요약하는 그래프이다.
#'대출건수', '도서건수' 열의 상자 수염 그림 그리기
plt.boxplot(ns_book7[['대출건수', '도서권수']])
plt.yscale('log')
plt.show()
#상자 수염 그림 수평으로 그리기 - vert 매개변수
plt.boxplot(ns_book7[['대출건수','도서권수']], vert=False)
plt.xscale('log')
plt.show()
#수염길이 조정하기1 - whis 매개변수
plt.boxplot(ns_book7[['대출건수','도서권수']], whis=10)
plt.yscale('log')
plt.show()
#수염길이 조정하기2 - whis 매개변수(백분율)
plt.boxplot(ns_book7[['대출건수','도서권수']], whis=(0,100))
plt.yscale('log')◾ vert 매개변수 : 기본값은 True, False로 수정하면 상자 수염 그림의 x-y축이 바뀐다.
◾ whis 매개변수 : 기본값은 1.5(IQR의 1.5배)이며, 10으로 바꾸면 IQR의 10배 범위로 수염 범위가 바뀐다. 소괄호() 안에 숫자를 지정하면 퍼센트 백분위수에 해당하는 데이터를 그릴 수 있다.
(상자 수염 그림은 코드 실행시 무한 로딩이 걸려서 확인해보지 못했다😭)
판다스의 그래프 함수
#산점도 그리기
ns_book7.plot.scatter('도서권수', '대출건수', alpha=0.1)
plt.show()
#히스토그램 그리기
ns_book7['도서명'].apply(len).plot.hist(bins=100)
plt.show()
#상자 수염 그림 그리기
ns_book7[['대출건수', '도서권수']].boxplot()
plt.yscale('log')
plt.show()
혼공학습단(혼자 공부하는 데이터 분석 with 파이썬) 4주차_기본 미션
5. ns_book7 남산도서관 대출 데이터에서 1980년~2022년 사이에 발행된 도서를 선택하여 다음과 같은 '발행년도' 열의 히스토그램을 그려보세요.
selected_rows = (ns_book7['발행년도'] >= 1980) & (ns_book7['발행년도'] <= 2022)
plt.hist(ns_book7.loc[selected_rows,'발행년도'])
plt.show()
혼공학습단(혼자 공부하는 데이터 분석 with 파이썬) 4주차_선택 미션
Ch.04(04-1)에서 배운 8가지 기술통계량(평균, 중앙값, 최솟값, 최댓값, 분위수, 분산, 표준편차, 최빈값)의 개념을 정리하기
◾ 평균 : 숫자 값을 모두 더해 개수로 나눈 것
◾ 중앙값 : 전체 데이터를 순서대로 늘어 놓았을 때 중앙에 위치한 값
◾ 최솟값 : 가장 작은 값.
◾ 최댓값 : 가장 큰 값
◾ 분위수 : 데이터를 순서대로 늘어 놓았을 때 이를 균등한 간격으로 나누는 기준점
◾ 분산 : 평균으로부터 데이터가 얼마나 퍼져있는지를 나타내는 값
◾ 표준편차 : 평균을 중심으로 데이터가 얼만큼 떨어져 분포해 있는지 표현하는 값
◾ 최빈값 : 데이터에서 가장 많이 등장하는 값
'자기계발 > Python' 카테고리의 다른 글
| [혼공단 9기] 6주차 : Chapter 06 복잡한 데이터 표현하기 (0) | 2023.02.17 |
|---|---|
| [혼공단 9기] 5주차 : Chapter 05 데이터 시각화하기 (0) | 2023.02.09 |
| [혼공단 9기] 3주차 : Chapter 03 데이터 정제하기 (4) | 2023.01.22 |
| [혼공단 9기] 2주차 : Chapter 02 데이터 수집하기 (2) | 2023.01.15 |
| [혼공단 9기] 1주차 : Chapter 01 데이터 분석을 시작하며 (0) | 2023.01.08 |